《高等数学学》课程思政优秀教学设计
“空间解析几何与向量代数—平面方程”
数学与信息科学学院（部） 鲍俊艳
课程名称：高等数学
课程性质：公共基础课
授课对象：本科
教学方式：启发式、探讨式
一、教学目标
1.价值目标
培养学生的爱国主义情怀、了解跨学科交融的价值、学习与探索、明辨性思维能力、职业素养、审美能力。
2.知识目标
记住并理解曲面方程、空间曲线的概念，记住并理解三种平面方程的表达式，能够分析三种平面方程之间的联系与区别，并会求平面方程。
3.能力目标
培养学生分析问题的能力，提高专业认知能力
二、教学内容分析
1.学情分析
授课对象是土木工程专业的学生，他们对建筑具有高度的鉴赏力。
2.教学重点
课程思政：培养学生的爱国主义情怀、跨学科交融的价值。
专业知识：三种平面方程的表示公式
3.教学难点
平面方程的三种表示公式及它们之间的联系
4.对重点、难点的处理
课程思政：课前布置阅读和查阅有关大兴国际机场资料的任务，让学生了解有关大型国际机场的国际地位，设计理念。通过材料的查阅，在课堂上让学生自己讲一讲自己通过查阅资料后的感受。
专业知识：通过层层递进的追问引出并解决问题，并通过小组讨论、老师点评的方式使学生深入理解平面方程的三种公式以及它们之间的联系。
三、课堂组织与实施
（图文并茂，语言简洁，2000字以内）
1.教学过程
第八章 空间解析几何与向量代数
——平面方程
（1）课前：布置阅读和查阅有关大兴国际机场资料的任务，让学生了解有关大兴国际机场的国际地位，设计理念。
（2）课中：
① 通过一组图片和引例引出本堂课的教学内容
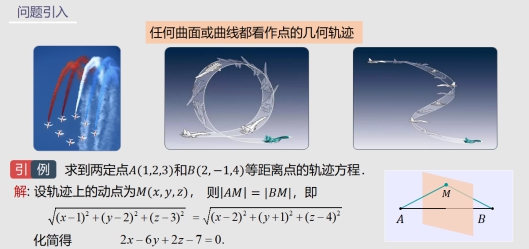
② 结合几何图形本堂课空间曲线和空间曲面的基本概念
③ 结合土木专业学生的特点，给出现实生活中应用空间曲面的实例——大兴国际机场。
在这部分内容中重点传递几个方面的信息并进行课程思政
◆ 数学与建筑的交叉融合建造出如此美妙的大兴国际机场，提高学生的学习兴趣，了解不同学科交叉的重要性，同时通过鉴赏扎哈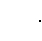
哈迪德的建筑作品，提高学生的鉴赏能力。
◆ 大兴国际机场的国际地位，彰显中国力量，激发学生的爱国主义情怀和实现强国之梦的担当。
④ 引入本节重点内容——平面方程
◆ 在这部分能内容中告诉学生解决问题要从简入繁——平面方程
曲面方程
◆ 通过层层递进的追问引出并解决问题，并通过小组讨论、老师点评的方式使学生深入理解平面方程的三种公式以及它们之间的联系。
同时，通过讨论能增强学生的团队协作意识。
⑤ 最后进行内容小结
通过三种平面方程公式的不同形式的观察，让学生分析哪种公式形式上更美，为什么？培养学生的数学素养。
2.教学方法
问题引导式、交流互动式、层层追问式、课堂讲授式
3.教学活动设计
课前任务布置：
◆ 让学生阅读和查阅有关大兴国际机场资料，了解有关大兴国际机场的国际地位，设计理念。通过材料的查阅书写自己的感受和反思。
◆ 以《中国学生发展核心素养》为导向，在课件的制作中，将课程内容中的句号转化成问号，将平铺直叙的教学方法转化为启发式教学,激发学生的学习兴趣。
授课过程：
◆ 通过问题引导式引出本堂课的内容。
◆ 找同学表述自己通过查阅大兴国际机场的相关资料后有哪些感受，其他同学可以自由发言进行补充和评判。这部分旨在培养学生的
◆ 通过层层追问的方式讲授平面方程的内容，提高学生的注意力，
◆ 课堂内容小结。在小结时让同学们找出所授内容之间的关联，同学们分组讨论并给出解决方法，加强对知识的理解和掌握，提高学生的数学素养，了解数学之美。
4.课程思政理念及分析
隐性课程思政：
课前认真备课，制作精良的课件，从颜色搭配，到动画的演示，都做到精益求精。
显性课程思政：
◆ 数学与建筑的交叉融合建造出如此美妙的大兴国际机场，提高学生的学习兴趣，了解不同学科交叉的重要性，同时通过鉴赏扎哈哈迪德的建筑作品，提高学生的鉴赏能力。
◆ 大兴国际机场的国际地位，彰显中国力量，激发学生的爱国主义情怀和实现强国之梦的担当。
四、教学效果分析
（评价与成效等，语言简洁，1000字以内）
学生通过查阅相关资料，并在课堂上讲述查阅资料后自己的收获和感受，增强学生的爱国主义情感。
通过北京大兴国际机场的设计与数学的融合，告诉学生只有多学科的交叉融合才能在创新中独辟蹊径。
层层追问方式的课堂讲授既能抓住学生的注意力，又体现了以学生为中心的教学理念。
在内容小结部分主要以提问的方式，让学生回答本堂课讲授的主要内容，进一步增强学生对所学内容的掌握。
在本堂课的最后，提出了更高的一个问题：三个平面方程之间的联系。让学生对所学内容能够举一反三。
通过观察三个公式的表达式，让学生从美学的角度出发，说一说那个公式形式比较美，比较美的公式的实用性怎么样？提高学生的评价能力和分析问题的能力。
